Nov 07 2009
Ma-temaatika
Pidasin sel nädalal MHG gümnaasiumiosale ettekande matemaatikast ja teaduslikust meetodist. Panen oma märkmed ka siia kirja.

Tere rahvas! Mul paluti siia täna suhteliselt vabal teemal rääkima tulla. Ja kui tegemist on vaba teemaga, siis üldiselt katsuvad inimesed ikka kõige lihtsama väljapääsu leida.
Aga mis on kõige lihtsam asi, millest rääkida? Enamasti on inimestel kõige lihtsam rääkida iseendast.
Tänase jutu teemaks olen seega mina ise, ehk siis minu temaatika ehk ma-temaatika. Ehk siis matemaatika minu elus.
Kes ma sihuke olen. 1995 lõpetasin Haapsalu Gümnaasiumi, 1999 Tartu Ülikooli. Kuni 2008 olin Microsoftis ja tegin tarkvara.
Austavaks ametinimetuseks oli mul tarkvarainsener, mis tähendas, et ma sain ise igasuguseid huvitavaid asju välja mõelda ja oma kätega midagi uut valmis teha. Mingil hetkel juhtub aga üsna sageli, et mingis grupis võetakse parim spetsialist ja pannakse ta teisi spetsialiste juhtima, nii juhtus ka minuga ja alates 2005 aastast olen ma tegelenud pigem teiste inimeste juhtimisega kui ise millegi valmistamisega.
2008 tulin Eestisse tagasi, praegu olen Webmedias ja juhin seal üht äriüksust. See tähendab, et mul on oma inimesed, oma eelarve, oma kliendid, oma tulud ja oma kulud.
Sellega seoses on vaja ka suurt hulka arvutamist, mille tulemusel leitakse enamasti üks konkreetne arv. See arv on minu üksuse kasum või kahjum.
Kui see arv on hea, siis on kõik hästi, sõidame Havaile puhkama ja oleme eluga rahul. Kui see arv ei ole hea, siis on kõik halvasti, inimesi tuleb lahti lasta ja üldse on kõik õnnetud.
Oluline on tähele panna, et tähtis pole mitte selle arvu tagantjärele välja rehkendamine, vaid pigem ennustamine, milliseks kujuneb tulemus järgmisel kuul, järgmisel kvartalil või järgmisel aastal, et meil oleks võimalik selle vastu mingeid konkreetseid samme astuda ja tulevikuks valmis olla. Tuleviku ennustamisel on meil aga tegemist väga paljude erinevate muutujatega ja nende erinevate koosmõjude kombinatsioone saab hinnata ainult mingit laadi statistilist analüüsi kasutades.
Lihtsustatult seega: mida parem matemaatikaoskus, seda parem ennustusvõime ja seda edukam äri.
Eelmine näide oli sellest, kuidas konkreetselt minul läheb vaja matemaatikat mingite konkreetsete ülesannete lahendamiseks. Sama näite võime aga tuua peaaegu suvalise muu eluala kohta. Igapäevastes toimingutes on meil kaks võimalust:
-Me kas teame, et mida teha, meil on selle jaoks mingi hulk reegleid, kuidas mingis konkreetses situatsioonis käituda. Me oskame vastata küsimusele “MIDA?” -Või me võime teada, et miks me midagi teeme, mis on liikumapanevad põhjused, millest need reeglid tulenevad. Me oskame vastata küsimusele “MIKS?”
Niikaua kui kõik on tavapärane, piisab esimesest lähenemisest, aga kui saabub mingi kriisisituatsioon, siis lihtsatest reeglitest enam ei piisa, siis ongi meil vaja vastust küsimusele “MIKS?”
Et MIKS küsimustele efektiivselt vastata, on vaja omada teadmisi selle ameti alusdistsipliinidest.
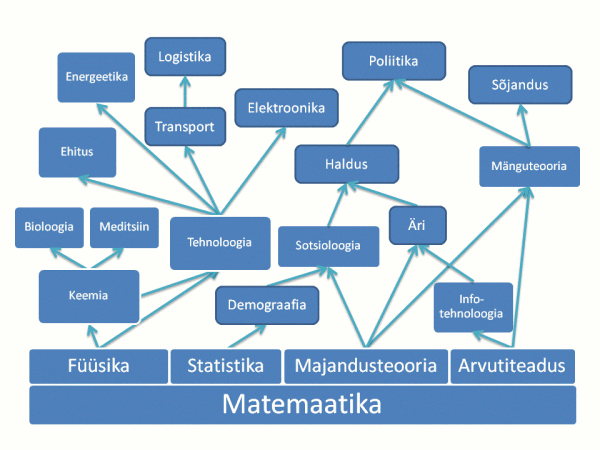
Oletame, et te tahate hakata presidendiks või mingiks muuks riigimeheks. Selleks, et selles ametis raskete olukordadega hakkama saada, on vaja tunda avaliku halduse põhimõtteid. Selleks aga, et tunda haldust, on vaja tunda sotsioloogiat ja äri. Nende jaoks on aga vaja tunda demograafiat, statistikat ja majandust. Ja niiviisi mööda ahelat edasi minnes jõuame mingil hetkel matemaatikani.
Oluline on see, et me ei kasuta matemaatikat mitte otse, vaid me kasutame selle rakendusi. Seega tuleb meil kindlasti mõista mitte ainult matemaatikat, vaid seda, mis toimub nende vahepealsete noolte sees – kuidas matemaatikat tegelikult ühes või teises teaduses ära kasutatakse ja kuidas neid teadusi omakorda igapäevaelus ära kasutatakse.

Samamoodi on meil võimalik mõelda ka kõigist muudest asjadest maailmas.
Esimeses lähenduses me võime olla rahul sellega, et asjad on niisugused nagu nad on.
Järgmise tasemena me võime mõelda sellest, et millised asjad veel olemas on?
Ja lõpuks võime mõelda sellest, et MIKS maailma asjad on just sellised nagu nad on?
Ja selle viimase MIKS küsimuse vastuse juurteni minnes jõuame väga tihti selleni, et matemaatika annab meile võtme oma küsimustele vastamiseks.
Ja kui meil on käes see võti maailma mõistmiseks, muutub meie elu ja asjadest arusaam tohutult rikkamaks ja rahuldust pakkuvamaks.

Räägime järgmiseks natuke filosoofilisemal teemal.
Ehk kust tulevad üldse meie teadmised?
Teadmisi on mitut laadi:
-Enda kogetud asjad
-Teistelt kuuldud asjad, näiteks see, mida vanemad lastele räägivad
-Olemasolevate teadmiste põhjal tõestatud ja põhjendatud asjad
Need kõik on kvalitatiivselt erinevad ja oluline on nende vahel vahet teha! Samuti on igal sellisel teadmisel usaldatavuse väärtus, mis sõltub teise kategooria puhul näiteks rääkija usaldatavusest ning kolmanda kategooria põhjal tuletusmeetodi korrektsusest ja rangusest.
Usaldatavuse seisukohalt on kõige olulisem teha vahet põhjendatud ja mittepõhjendatud väidete vahel.
Matemaatika on selles osas ideaalne, et matemaatikas ei võeta ühtki väidet tõena, kui ta pole enne põhjendatud ja tõestatud.
Võtame kasvõi sellise lihtsa näite nagu Pythagorase teoreem.
Kui meile lihtsalt väidetakse, et täisnurkses kolmnurgas a2+b2=c2, siis me võime seda lihtsalt uskuda või alternatiivina võime küsida tõestust. Õnneks on matemaatikas väidetel üldjuhul olemas tõestused ja põhjendused. Ja Pythagorase teoreemi saame tõestada üsna lihtsal viisil:

Seega tekitab matemaatika inimeses harjumuse erinevaid väiteid kontrollida ja põhjendada.
Matemaatika vastandiks on selles mõttes religioon. Religioonis öeldakse meile, et me lihtsalt peame mingit asja uskuma ja kõik. Ja kui me ei usu, siis läheme põrgusse. Kasvõi Martin Luther on öelnud, et mõistus on usu suurim vaenlane.
Seal vahepeal on aga veel hulk võimalusi igasugustest väidetest, mille esitajad (nt poliitikud või müügimehed) tulevad ja räägivad meile targa ja veenva näoga, et asjad on just nimelt mingil konkreetsel viisil, aga nad ei põhjenda seda kuidagi! Või siis põhjendavad puudulikult.
Kui me oleme harjunud väidete kontrollimisel matemaatilise rangusega, siis saame ka:
a)Kontrollida, kas meie oponent esitab oma väiteid korrektselt .
b)Leida nendes väidetes vastuolusid.
Mõned näited, millega ma ise olen kokku puutunud:
Näide 1: homöopaatia. Võetakse mingi toimeaine, lahjendatakse seda veega pooleks ja loksutatakse. Siis lahjendatakse jälle ja loksutatakse. Ja nii näiteks 30 (või 60 või 200) korda järjest. Mida rohkem, seda uhkem. Matemaatiliselt saame kerge vaevaga aru, et tulemis pole tõenäoliselt enam mitte ainsatki esialgse aine molekuli, aga inimesed, kes matemaatikat ei tunne, ostavad ikka.
Näide 2: kinnisvarakrahh. Paljud inimesed väitsid tõsise näoga, et kinnisvarahinnad ainult tõusevad ja muud moodi ei olegi üldse võimalik. Ja teised uskusid, hoolimata sellest, et lihtne arvutus näitab, et selline kasv pole majanduslikult jätkusuutlik. Ja võtsid suuri laene eeldusel, et mõne aasta pärast müüvad oma korteri tohutu kasumiga maha ja maksavad laenud tagasi.
Näide 3: puhkuseosakud. Olen juhtunud paarile puhkuseosakute müügiüritusele, kus müügimees veenva näoga seletab, kui hea diiliga ikka tegemist on. Joonistab tahvlile arvusid ja “tõestab”, kui palju raha ma sellega ikka kokku hoian. Mina näen muidugi läbi, et ühes tulbas on arvud inflatsiooniga läbi korrutatud ja teises mitte, selle peale teeb kähku teist juttu. Aga kõrval inimesed ostavad ja kiidavad. Mõni aeg hiljem aga avastavad, kuidas hulk inimesi üritab eBayl meelehetilikult neist osakutest lahti saada.

Ma näen siin saalis mitut matemaatikaõpetajat. Matemaatikaõpetajatelt küsitakse ilmselt tihti, et miks ma pean neid ülesandeid lahendama kogu aeg? Mis mul sellest päris elus kasu on?
Kehalise kasvatuse õpetajad panevad samas näiteks poisse kätekõverdusi tegema. Mis meil sellest päris elus kasu on? Kätekõverduste puhul on vastus küllaltki otsene – see teeb inimest tugevamaks ja ta jaksab päris elus paremini sooritada sarnaseid tegevusi, kus kätejõudu vaja läheb.
Matemaatikaülesannetel on samasugune efekt inimese aju treenimisel. Tegelikus elus koosneb minu enda töö pidevast ülesannete lahendamisest. Mõned näited sedalaadi ülesannetest:
-Hinnang, kui kaua mingi projekt aega võiks võtta
-Hinnang, kui palju me järgmisel kuul raha teenime
Need on puhtalt arvutuslikud ülesanded. Aga on ka selliseid ülesandeid:
-programm töötab praegu liiga keeruliselt – tehke ta lihtsamaks
-programm on aeglane, tehke ta kiiremaks
Ehk siis ülesanded, kus meil pole isegi mitte täpne valem teada, kuidas sellisele ülesandele üldse läheneda. Me peame ise välja mõtlema, millist valemit kasutada, milliseid parameetreid seal rakendada.
Ja siis on veel ülesanded nagu:
- Ma tahaksin, et sinu osakond teeniks rohkem raha
-Tee nii, et inimestel oleks sinu organisatsioonis parem töötada
Selliseid suureemaid ja väiksemaid ülesandeid tuleb minu ette iga päev ridamisi. Ja ainuke võimalus nendega hakkama saamiseks on omada piisavalt hästi ülesannete lahendamiseks treenitud mõistust, nii et ma saan kiiresti võtta: ülesanne->lahendus, ülesanne->lahendus, ülesanne->lahendus.
Muuseas: vahet tuleb teha harjutusel ja ülesandel. Lihtsalt tulpades võrrandite lahendamine on harjutus. Tekstülesanne, kus valem pole ette antud, on oluliselt kasulikum!

Paljud asjad matemaatikas on kasutatavad väga mitmel eri moel. Näiteks võrrandite lahendamine on osaks praktiliselt kõigist matemaatika rakendusaladest.
Kui me oskame mitmesuguseid erinevaid võrrandeid lahendada, on nad meile abiks igal pool, arhitektuurist ärijuhtimiseni.
Üks ja seesama matemaatiline MUDEL on kasutusel väga paljudes eri valdkondades.
Seega, matemaatika on nagu keeleõpe:
kui me õpime ennast mingis keeles väljendama, on meil võimalik kirja panna lõputult erinevaid mõtteid, üksikutest lausetest kuni paksude raamatuteni.
Ja kui me õpime matemaatika keelt oma elus kasutama, on meil samuti lõputult võimalusi seda erinevates kontekstides ära kasutada.

Kokkuvõtteks:
-Maailm põhineb ühel või teisel viisil matemaatikal.
-Matemaatika mõistmine on võti maailma mõistmiseks (või vähemalt korrektseks mõistmiseks, on ka teisi filosoofiaid, mis annavad meile ebakorrektseid tulemusi).
-Matemaatika harjutamine loob eeldused elus tekkivate probleemide lahendamiseks.
Sekka küsiti mult veel mitmesuguseid lõbusaid küsimusi:
Küsimus: kas Kuu peale on mõistlik maatükki osta?
Vastus: Igasuguse investeeringu puhul on meil tegemist matemaatilise mudeliga, mis peegeldab mingit laadi reaalsust. Mul on näiteks natuke Microsofti aktsiaid ja Brasiilia riigi võlakirju, mis peegeldavad vastavalt seda, kuidas Microsoftil ja Brasiilial tulevikus läheb. Kui neil läheb hästi, läheb ka minu investeeringul hästi, aga oluline on kasutada eelpool toodud usaldatavuse mõõdikuid ehk siis ise aru saada, kas vastav majanduslik mudel tegelikult paika peab või ei, mitte lihtsalt müügimehe juttu uskuda. Kuu majandusliku tuleviku osas olen skeptiline.
Küsimus: aga kas me saame tegelikult uskuda, et Martin Luther niiviisi ütles?
Vastus: Ainsad a priori usaldatavad väited on matemaatilised tulemused. Kõigi muude kohta kehtib usaldatavuse hinnang, mis on <100%. Kuna aga antud juhul oli tegemist minu jaoks usaldusväärse allikaga, hindan ma selle tsitaadi korrektsuse tõeväärtust kõrgeks.
Küsimus: kas armastus on ka matemaatilise mudeli järgi hinnatav?
Vastus: Armastus tähendab tegelikult seda, et mõni isik tundub meile subjektiivselt tohutult parem ja väärtuslikum kui teised. Loogiliselt võttes inimeste vahel muidugi nii suuri erinevusi ei ole. Bioloogiliselt soodustab armastuse olemasolu aga monogaamsete suhete tekkimist ja selle läbi liigi püsimist. Seega on armastamise võimelistel isenditel geneetiline eelis ja armastus kui fenomen on tekkinud loodusliku valiku tagajärjel. OLULINE: see ei tähenda, et armastus ei oleks hea ja tore. See, kui me suudame mingit fenomeni teaduslikult põhjendada, ei kahanda kuidagi selle emotsionaalset väärtust, täpselt nagu päikeseloojangu värvide füüsikaline selgitus ei tee seda kuidagi vähem ilusamaks ![]()
Küsimus: Inimesed mõistavad maailma praegu hoopis teisiti kui tuhat aastat tagasi. Kas meie praegune teaduslik mudel ei ole tuhande aasta pärast täpselt samamoodi aegunud kui praegu tuhande aasta vanune?
Vastus: Teadusliku meetodi eripära on see, et teaduslikud tulemused on falsifitseeritavad ja kolmandatel osapooltel peab olema võimalik nende kehtivust või mittekehtivust sõltumatult kontrollida. Tuhat aastat tagasi oli teadusliku meetodi alusel ära kirjeldatud väga väike osa maailmast, aga see osa, mis oli teaduslikult kirjeldatud, peab suures osas praegugi paika. Praegu on inimeste teaduslik arusaam laienenud ja ma olen optimistlik ka praeguste tulemuste säilimise osas tuhande aasta pärast.
